書評

　算数は同じ理由で好きと嫌いが分かれます。
「答えが一つに決まっているから、とてもすっきりしていて好き」、「いや、公式に当てはめるだけのあんな窮屈な勉強は嫌いだ」と。
　皆さんはどうですか。
　算数の問題は、本当にいつも答えが一つに決まっているのでしょうか。本当に窮屈な勉強なのでしょうか。
　出来上がったものをしっかり覚えて、後はそれに当てはめて解けばいいのでしょうか。もしそんな勉強であれば、当然、面白くない。
　もちろん、解き方は多様です。
　そして時には答えも一つに決まらない場合がある。オープンエンドと言われる問題がそれです。
　また、問題も教科書や問題集、あるいは先生が出すばかりではない。自らの力でもつくることができる。つくるといっても、一つの問題を解いて終わりにしないで、「もしも～だったらどうか」と考えて、場を広げていくのです。
　そんな自由な勉強が算数なのです。
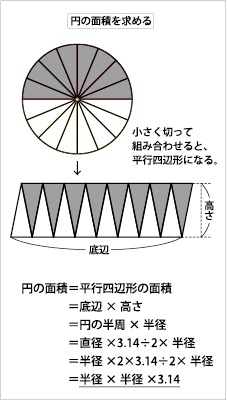
　円の面積の求め方を考えてみましょう。「半径×半径×３・１４」。こんな公式が教科書に載っています。なぜこのような公式が生まれたのでしょうか。まず、円を蜜柑（みかん）の断面のように切って、面積の求め方を知っている平行四辺形に並べ替えると、「底辺×高さ」が「円の半周×半径」と変形されます。円周が直径の何倍になっているかを表す数「円周率（３・１４）」を使い、この式を変えると、「直径×３・１４÷２×半径」となり、さらに、直径を半径×２におきかえて「半径×２×３・１４÷２×半径＝半径×半径×３・１４」となるわけです。

　さて、この式変形を見て、直径と半径の両者が登場した時に、なぜ半径に統一したのでしょう。なぜ直径を使わなかったのでしょう。こんなことを考えたことありますか。もしも直径にしてみたら――「直径×３・１４÷２×直径÷２」となりますね。すると「直径×直径×０・７８５」。これも公式。昔の文献では、この０・７８５を「円積率」と呼んでいました。円に外接する正方形に対して円の面積が78・５％だと言うわけ。面白い見方です。
　こんな自由な学びが算数なのです。
「分数÷分数」の計算、後ろをひっくり返してかけるなんて決まったことなのか。分子は分子でわる。分母は分母でわる。これでできないか。分数は大きさが同じで表現を変えることはいくらでもできます。１／２でも２／４でもいいということです。それを使えば、違った方法が見つかる。自分で方法を見つけ出すなんてとっても面白いことです。
　ちょっと周りを見てごらんなさい。身のまわりには算数がいっぱい。今日の新聞、重なっている紙をばらばらにしてみると、見開きのページの合計はどれも同じ。おやっ、なぜでしょう。
　この不思議の解明は算数の役目です。
『算数のしくみ大事典』は、そんな不思議の解明がいっぱい詰まっている本です。用語には英語も付けました。言葉は違っていても、算数の式や記号は世界共通だからです。
　算数は自由。なんとすばらしいものではありませんか。

　（つぼた・こうぞう　青山学院大学特任教授）